By Ion Saliu, Founder of Blackjack Mathematics

I. Probability, Odds for a Blackjack or Natural 21
II. House Edge on Insurance Bet at Blackjack
III. Calculate Double-Down Hands
IV. Calculate Blackjack Pairs: Strict or Mixed Ten-Cards
V. Free Blackjack Resources, Basic Strategy, Casino Gambling Systems

1.1. Calculate Probability (Odds) for a Blackjack or Natural 21

The odds of getting a natural blackjack are, undoubtedly, 1 in 21 hands (a hand consisting of exactly 2 cards). Such a case is non-existent in real-life gambling, however. There are at least TWO participants in a blackjack game: Dealer and one player. Is the probability for a natural blackjack the same – regardless of number of participants? Probability Of Winning Blackjack Lesson of online casinos and casino player forum. Note that we are an informational resource only, featuring reviews and recommendations of casinos, games, and bonuses. We are not a casino and no gambling with real money takes place on this site. P both = P blackjack × 3 × 15 ( 50 2). By the inclusion/exclusion principle, the probability of at least one getting blackjack is the sum of probabilities of each individual getting blackjack minus the probability of both getting blackjack (removes redundant overlap): 1 − P either or both = 0.90524. Remember: in blackjack, your chances of winning or busting will change each time a card is removed from the deck. In Example 1, the probability of the dealer going bust on their next card is 19.98%. But players win with 20 a lot more often than they lose, with about 70.2 percent of player 20s winning, 12.2 percent losing and 17.6 percent pushing. Twenty is a profitable hand for players against every dealer face up card. Let’s look at player 10-10 vs. Each dealer possibility in a six-deck game in which the dealer hits soft 17.

First capture by the WayBack Machine (web.archive.org) Sectember (Sect Month) 1, 2015.

I have seen lots of search strings in the statistics of my Web site related to the probability to get a blackjack (natural 21). This time (November 15, 2012), the request (repeated 5 times) was personal and targeted directly at yours truly:

• 'In the game of blackjack determine the probability of dealing yourself a blackjack (ace face-card or ten) from a single deck. Show how you arrived at your answer. If you are not sure post an idea to get us started!'

Oh, yes, I am very sure! As specified in this eBook, the blackjack hands can be viewed as combinations or arrangements (the order of the elements counts; like in horse racing trifectas).

1) Let's take first the combinations. There are 52 cards in one deck of cards. There are 4 Aces and 16 face-cards and 10s. The blackjack (or natural) can occur only in the first 2 cards. We calculate first all combinations of 52 elements taken 2 at a time: C(52, 2) = (52 * 51) / 2 = 1326.

We combine now each of the 4 Aces with each of the 16 ten-valued cards: 4 * 16 = 64.

The probability to get a blackjack (natural): 64 / 1326 = .0483 = 4.83%.

2) Let's do now the calculations for arrangements. (The combinations are also considered boxed arrangements; i.e. the order of the elements does not count).

We calculate total arrangements for 52 cards taken 2 at a time: A(52, 2) = 52 * 51 = 2652.

In arrangements, the order of the cards is essential. Thus, King + Ace is distinct from Ace + King. Thus, total arrangements of 4 Aces and 16 ten-valued cards: 4 * 16 * 2 = 128.

The odds to get a blackjack (natural) as arrangement: 128 / 2652 = .0483 = 4.83%.

4.83% is equivalent to about 1 in 21 blackjack hands. (No wonder the game is called Twenty-one!)

Calculations for the Number of Cards Left in the Deck, Number of Decks

There were questions regarding the number of cards left in the deck, number of decks, number of players, even the position at the table.

1) The previous probability calculations were based on one deck of cards, at the beginning of the deck (no cards burnt). But we can easily calculate the blackjack (natural) odds for partial decks, provided that we know the number of remaining cards (total), Aces and Ten-Value cards.

Let's take the situation heads-up: One player against the dealer. Suppose that 12 cards were played, including 2 Tens; no Aces out. What is the new probability to get a natural blackjack?

Total cards remaining (R) = 52 - 12 = 40

Aces remaining in the deck (A): 4 - 0 = 4

Ten-Valued cards remaining (T): 16 - 2 = 14

Odds of a natural: (4 * 14) / C(40, 2) = 56 / 780 = 7.2%

(C represents the combination formula; e.g. combinations of 40 taken 2 at a time.)

The probability for a blackjack is higher than at the beginning of a full deck of cards. The odds are exactly the same for both Player and Dealer. But - the advantage goes to the Player! If the Player has the BJ and the Dealer doesn't, the Player is paid 150%. If the Dealer has the blackjack and the Player doesn't, the Player loses 100% of his initial bet!

This situation is valid only for one Player against casino. Also, this situation allows for a higher bet before the round starts. For multiple players, the situation becomes uncontrollable. Everybody at the table receives one card in succession, and then the second card. The bet cannot be increased during the dealing of the cards. Hint: try as much as you can to play heads-up against the Dealer!

The generalized formula is:

Probability of a blackjack: (A * T) / C(R, 2)

A = Aces in the deck

T = Tens in the deck

R = Remaining cards in the deck.

2) How about multiple decks of cards? The calculations are not exactly linear because of the combination formula. For example, 2 decks, (104 cards):

~ the 2-deck case:

C(52, 2) = 1326

C(104, 2) = 5356 (4.04 times larger than total combinations for one deck.)

8 (Aces) * 32 (Tens) = 256

Odds of BJ for 2 decks = 256 / 5356 = 4.78% (a little lower than the one-deck case of 4.83%).

~ the 8-deck case, 416 total cards:

C(52, 2) = 1326

C(416, 2) = 86320 (65.1 times larger than total combinations for one deck.)

32 (Aces) * 128 (Tens) = 4096

Odds of BJ for 8 decks = 4096 / 86320 = 4.75% (a little lower than the two-deck situation and even lower than the one-deck case of 4.83%).

There are NO significant differences regarding the number of decks. If we round the figures, the general odds to get a natural blackjack can be expressed as 4.8%.

The advantage to the blackjack player after cards were played: Not nearly as significant as the one-deck situation.

3) The position at the table is inconsequential for the blackjack player. Only heads-up and one deck of cards make a difference as far the improved odds for a natural are concerned.

• Axiomatic one, let's cover all the bases, as it were. The original question was, exactly, as this: 'Dealing yourself a blackjack (Ace AND Face-card or Ten) from a single deck'. The calculations above are accurate for this unique situation: ONE player dealing cards to himself/herself. The odds of getting a natural blackjack are, undoubtedly, 1 in 21 hands (a hand consisting of exactly 2 cards).
• Such a case is non-existent in real-life gambling, however. There are at least TWO participants in a blackjack game: Dealer and one player. Is the probability for a natural blackjack the same – regardless of number of participants? NOT! The 21 hands (as in probability p = 1 / 21) are equally distributed among multiple game agents (or elements in probability theory). Mathematics — and software — to the rescue! We apply the formula known as exactly M successes in N trials. The best software for the task is known as SuperFormula (also component of the integrated Scientia software package).
• Undoubtedly, your chance to get a natural BJ is higher when playing heads-up against the dealer. The degree of certainty DC decreases with an increase in the number of players at the blackjack table. I did a few calculations: Heads-up (2 elements), 4 players and dealer (5 elements), 7 players and dealer (8 elements).
  • The degree of certainty DC for 2 elements (one player and dealer), one success in 2 trials (2-card hands) is 9.1%; divided by 2 elements: the chance of a natural is 9.1% / 2 = 4.6% = the closest to the 'Dealing yourself a blackjack (Ace AND Face-card or Ten) from a single deck' situation.
  • The chance for 5 elements (4 players and dealer), one success in 5 trials (2-card hands) is 19.6%; distributed among 5 elements, the degree of certainty DC for a blackjack natural is 19.6% / 5 = 3.9%.
  • The probability for 8 elements (7 players and dealer), one success in 8 trials (2-card hands) is 27.1%; equally distributed among 8 elements, the degree of certainty DC of a blackjack natural is 27.1% / 8 = 3.4%.
• That's mathematics and nobody can manufacture extra BJ natural 21 hands... not even the staunchest and thickest card-counting system vendors! The PI... er, pie is small to begin with; the slices get smaller with more mouths at the table. Ever wondered why the casinos only offer alcohol for free — but no pizza?

1.2. Probability, Odds for a Blackjack Playing through a Deck of Cards

The probabilities in the first chapter were calculated for one trial. That is, the odds to get a blackjack in the first two cards. But what are the probabilities to get a natural 21 dealing an entire deck?

1.2.A. Dealing 2-card hands until the deck is dealt entirely

There are 52 cards in the deck. Total number of trials (2-card hands) is 52 / 2 = 26. SuperFormula probability software does the following calculation:

• The probability of at least one success in 26 trials for an event of individual probability p=0.0483 is 72.39%.

1.2.B. Dealing 2-card hands in heads-up play until the deck is dealt entirely

There are 52 cards in the deck. We are now in the simplest real-life situation: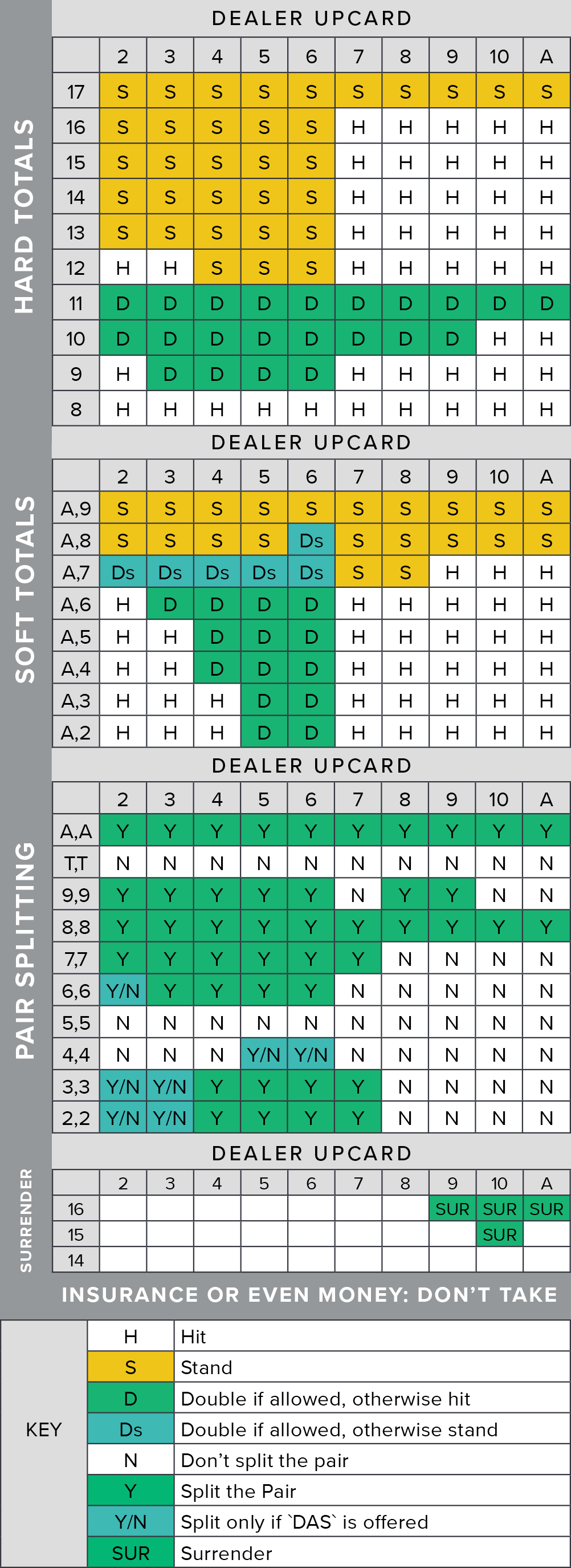 heads-up play. There is one player and the dealer in the game. We suppose an average of 6 cards dealt in one round. Total number of trials in this case is equivalent to the number of rounds played. 52 / 6 makes approximately 9 rounds per deck. SuperFormula does the following calculation:

• The probability of at least one success in 9 trials for an event of individual probability p=0.0483 is 35.95%.

You, the player, can expect one blackjack every 3 decks in heads-up play.

2. House Edge on the Insurance Bet at Blackjack

“Insurance, anyone?” you can hear the dealer when her face card is an Ace. Players can choose to insure their hands against a potential dealer's natural. The player is allowed to bet half of his initial bet. Is insurance a good side bet in blackjack? What are the odds? What is the house edge for insurance? As in the case of calculating the odds for a natural blackjack, the situation is fluid. The odds

Probability Of Winning Blackjack

and therefore the house edge are proportionately dependent on the amount of 10-valued cards and total remaining cards in the deck.

We can devise precise mathematical formulas based on the Tens remaining in the deck. We know for sure that the casino pays 2 to 1 for a successful insurance (i.e. the dealer does have Ten as her hole card).

We start with the most easily manageable case: One deck of cards, one player, the very beginning of the game. There is a total of 16 Teens in the deck (10, J, Q, K). The dealer has dealt 2 cards to the player and one card to herself that we can see exactly — the face card being an Ace. Therefore, 52 – 3 = 49 cards remaining in the deck. There are 3 possible situations, axiomatic one:

• 1) The player has 2 non-ten cards; there are 16 Teens in the deck = the favorable situations to the player if taking insurance. There are 49 – 16 = 33 unfavorable cards to insurance. However, the 16 favorable cards amount to 32, as the insurance pays 2 to 1. The balance is 33 – 32 = +1 unfavorable situation to the player but favorable to the casino (the + sign indicates a casino edge). In this case, there is a house advantage of 1/49 = 2%.
• 2) The player has 1 Ten and 1 non-ten card; there are 15 Teens remaining in the deck = the favorable situations to the player if taking insurance. There are 49 – 15 = 34 unfavorable cards to insurance. However, the 15 favorable cards amount to 30, as the insurance pays 2 to 1. The balance is 34 – 30 = +4 unfavorable situations to the player but favorable to the casino. In this case, there is a house advantage of 4/49 = 8%.
  • This can be also the case of insuring one's blackjack natural: an 8% disadvantage for the player.
  • This figure of 8% represents the average house edge regarding the insurance bet. I did calculations for various situations — number of decks and number of players.
• 3) The player has 2 Ten-count cards; there are 14 Teens in the deck = the favorable situations to the player if taking insurance. There are 49 – 14 = 35 unfavorable cards to insurance. However, the 14 favorable cards amount to 28, as the insurance pays 2 to 1. The balance is 35 – 28 = +7 unfavorable situations to the player but favorable to the casino. In this case, there is a house advantage of 7/49 = 14%. This is the worst-case scenario: The player should never — ever — even think about insurance with that strong hand of 2 Tens!

Believe it or not, the insurance can be a really sweet deal if there are multiple players at the blackjack table! Let's say, 5 players, the very beginning of the game. There is a total of 16 Teens in the deck (10, J, Q, K). The dealer has dealt 10 cards to the players and one card to herself that we can see exactly — the face card being an Ace. Therefore, 52 – (10 + 1) = 41 cards remaining in the deck. There are many more possible situations, some very different from the previous scenario:

• 1) The players have 10 non-ten cards; there are still 16 Tens in the deck = the favorable situations to the player if taking insurance. There are 41 – 16 = 25 unfavorable cards to insurance. However, the 16 favorable cards amount to 32, as the insurance pays 2 to 1. The balance is 25 – 32 = –7 favorable situation to the player but unfavorable to the casino (the – sign indicates a player advantage now). In this case, there is a house advantage of 7/41 = –17%. The Player has a whopping 17% advantage if taking insurance in a case like this one!
• 2) The players have 10 Ten-count cards; there are 6 Teens in the deck = the favorable situations to the player if taking insurance. There are 41 – 6 = 35 unfavorable cards to insurance. However, the 6 favorable cards amount to 12, as the insurance pays 2 to 1. The balance is 35 – 12 = +23 unfavorable situations to the player but favorable to the casino. In this case, there is a house advantage of 23/41 = 56%. This is the worst-case scenario: None of the players should ever even think about insurance with those strong hands of 2 Tens per capita!
• 3) Applying the wise aurea mediocritas adagio, there should be an average of 3 or 4 Teens coming out in 11 cards; thus, 12 or 13 Tens remaining in the deck. There are 41 – 13 = 28 unfavorable cards to insurance. However, the 12.5 favorable cards amount to an average of 25, as the insurance pays 2 to 1. The balance is 30 – 25 = +5 unfavorable situations to the player but favorable to the casino. In this case, there is a house advantage of 5/41 = 12%. Unfortunately, even if we consider averages, taking insurance is a repelling bet for the player.

A formula? It would look complicated symbolically, but it is very easy to follow.

HA = {(R – T) – T*2} / R

where —

• HA = house advantage
• R = cards remaining in the deck
• T = Tens remaining in the deck.

• Axiomatic one, buying (taking) insurance can be a favorable bet for all blackjack players, indeed. Of course, under special circumstances — if you see certain amounts of ten-valued cards on the table. The favorable situations are calculated by the formula above.
But, then again, a dealer natural 21 occurs about 5%- of the time — the insurance alone won't turn the blackjack game entirely in your favor.

3. Calculate Blackjack Double-Down Hands

Strictly-axiomatic colleague of mine, writing software leads me into new-ideas territory far more often than not. I discovered something new and intriguing while programming software to calculate the blackjack odds totally mathematically. By that I mean generating all possible elements and distinguishing the favorable elements. After all, the formula for probability is the rapport of favorable cases, F, over total possible cases, N: p = F/N.

Up until yours truly wrote such software, total elements in blackjack (i.e. hands) were obtained via simulation. Problem with simulation is incomplete generation. According to by-now famed Ion Saliu's Probability Paradox, only some 63% of possible elements are generated in a simulation of N random cases.

I tested my software a variable number of card decks and various deck compositions. I noticed that decks with lower proportions of ten-valued cards provided higher percentages of potential double-down hands. It is natural, of course, as Tens are the only cards that cannot contribute to a hand to possibly double down. However, the double-down hands provide the most advantageous situations for blackjack player. Indeed, it sounds like 'heresy' to all followers of the cult or voodoo ritual of card counting!

I rolled up my sleeves and performed comprehensive calculations of blackjack double-downs (2-card hands). The single deck is mostly covered, but the calculations can be extended to any number of decks.

At the beginning of the deck (shoe): Total combinations of 52 cards taken 2 at a time is C(52, 2) = 1326 hands. Possible 2-card combinations that can be double-down hands:

• 9-value cards AND 2-value cards: 4 9s * 4 2s = 16 two-card possibilities
• 8-value cards AND 2-value cards: 4 8s * 4 2s = 16 two-card configurations
• 8-value cards AND 3-value cards: 4 8s * 4 3s = 16 two-card possibilities
• 7-value cards AND 2-value cards: 4 7s * 4 2s = 16 two-card configurations
• 7-value cards AND 3-value cards: 4 7s * 4 3s = 16 two-card possibilities
• 7-value cards AND 4-value cards: 4 7s * 4 4s = 16 two-card configurations
• 6-value cards AND 3-value cards: 4 6s * 4 3s = 16 two-card configurations
• 6-value cards AND 4-value cards: 4 6s * 4 4s = 16 two-card combinations
• 6-value cards AND 5-value cards: 4 6s * 4 5s = 16 two-card possibilities
• 5-value cards AND 4-value cards: 4 5s * 4 4s = 16 two-card combinations
• 5-value cards AND 5-value cards: C(4, 2) = 6 two-card hands (5 + 5 can appear 6 ways).
• Ace AND 2-value cards: 4 As * 4 2s = 16 two-card combinations
• Ace AND 3-value cards: 4 As * 4 3s = 16 two-card possibilities
• Ace AND 4-value cards: 4 As * 4 4s = 16 two-card hands
• Ace AND 5-value cards: 4 As * 4 5s = 16 two-card possibilities
• Ace AND 6-value cards: 4 As * 4 6s = 16 two-card hands
• Ace AND 7-value cards: 4 As * 4 7s = 16 two-card combinations.
• Total possible 2-card hands in doubling down configuration: 262. Not every configuration can be doubled down (e.g. 4+5 against Dealer's 9 or A+2 against 7).
• We look at a double down blackjack basic strategy chart. Some 42% of the hands ought to be doubled-down (strongly recommended): 262 * 0.42 = 110. That figure represents 8% of total possible 2-hand combinations (1362), or a chance equal to once in 12 hands.
• The chance for double-down situations increases with an increase in tens out over the one third cutoff count. The probability for a natural blackjack decreases also — one reason the traditional plus-count systems anathema the negative counts. But what's lost in naturals is gained in double downs — and then some.
• A sui generisblackjack card-counting strategy was devised by yours truly and it beats the traditionalist plus count systems hands down, as it were.
• Be mindful, however, that nothing beats the The Best Casino Gambling Systems: Blackjack, Roulette, Limited Martingale Betting, Progressions. That's the only way to go, the tao of gambling.

4. Calculate Blackjack Pairs: Strict or Mixed Ten-Cards

The odds-calculating software I mentioned above (section III) also counts all possible blackjack pairs. The software, however, considers pairs to be two cards of the same value. In other words, 10, J, Q, K are treated as the same rank (value). My software reports data as this fragment (single deck of cards):

Mixed Pairs: All 10-Valued Cards Taken 2 at a Time

Evidently, there are 13 ranks. Nine ranks (2 to 9 and Ace) consist of 4 cards each (in a single deck). Four ranks (the Tenners) consist of 16 cards. Total of mixed pairs is calculated by the combination formula for every rank. C(4, 2) = 6; 6 * 9 = 54 (for the non-10 cards). The Ten-ranks contribute: C(16, 2) = 120. Total mixed pairs: 54 + 120 = 174. Probability to get a mixed pair: 174 / 1326 = 13%.

Strict Pairs: Only 10+10, J+J, Q+Q, K+K

Probability Of Blackjack Single Deck

But for the purpose of splitting pairs, most casinos don't legitimize 10+J, or

Blackjack Probability Theory

Q+K, or 10+Q, for example, as pairs. Only 10+10, J+J, Q+Q, K+K are accepted as pairs. Allow me to call them strict pairs, as opposed to the above mixed pairs.

There are 13 ranks of 4 cards each. Each rank contributes C(4, 2) = 6 pairs. Total strict pairs: 13 * 6 = 78. Probability to get a mixed pair: 78 / 1326 = 5.9%.Total strict pairs = 78 2-card hands (5.9%, but...).

However, not all blackjack pairs should be split; e.g. 10+10 or 5+5 should not be split, but stood on or doubled down. Only around 3% of strict pairs should be legitimately split. See the optimal split pairsblack jack strategy card.

5. Free Blackjack Resources, Basic Strategy, Casino Gambling Systems

• Blackjack Mathematics Probability Odds Basic Strategy Tables Charts.
• The Best Blackjack Basic Strategy: Free Cards, Charts.
  ~ All playing decisions on one page — absolutely the best method of learning Blackjack Basic Strategy (BBS) quickly (guaranteed and also free!)
• Blackjack Gambling System Based on Mathematics of Streaks.
• Blackjack Card Counting Cult, Deception in Gambling Systems.
• The Best Blackjack Strategy, System Tested with the Best Blackjack Software.
• Reality Blackjack: Real, Fake Odds, House Advantage, Edge.

Back to Forums IndexSocrates HomeSearch

Probability Of Getting A Blackjack

Blackjack is undoubtedly one of the most preferred game to play casinos world-wide. Things have been this way for several centuries now. This game of strategy became famous because of the regular wins in the game. Now we take a look at whether the success in the game is real or its just wishful thinking by real money gamblers. This is easily done by exploring the figures which paint a clear picture of what actually happens.

Blackjack Odds: TheFigures

Just likeany other real casino game, the game of blackjack has odds that can becalculated. It is possible to determine the probability of an event occurringwith a certain amount of accuracy. This becomes easier and more accurate whenthe event occurs several thousands of time. Since the game of blackjack played several millions of times daily it iseasy to gather data which is analyzed to give the odds.

The goodthing is that blackjack has been around for several hundreds of years.Therefore we do not need to do the complex statistical calculations. Using theZ-statistic together with the central limit theorem is sufficiently difficult.

The Actual figure

Eachvariety of the game has its own odds, however, there are some generalizationsthat can be made. There have been a lot of people that have spent a lot of timestudying the game of blackjack in order to find the best way to beat the house.Their research has come up with some interesting figures.

Dependingon the variety that you choose to play the probability of getting a win isbetween 42% and 43%. The game can also end in a draw.Odds of that happening are usually below 9% for most versions of the game. Whenyou eliminate the possibility of “pushing” or “draw” the odds of getting a winjumps to above 45%.

The chancesof the house winning are larger than that of the player winning. Again it isessential to mention again that these odds are derived after a large number ofgames played. Millions of hands were used to come up with these statistics. Thehouse is likely to win up to 49% of the time.

According to mobile sports betting casinos , odds for going bust are determined by the rules of the variety of blackjack being played. For games that allow the dealer stand at a hard 17 the probability of the dealer busting is higher than in a game where the dealer stands at a soft 17. The odds of the dealer busting in both cases are around 28%. The player is less likely to bust than the dealer. This improves the players’ odds of getting a win. Players are about 60% less likely to bust when compared to dealers.

Why it is Difficult toBeat the House in Blackjack

Naturally,the casino whether online or land-based has to improve the odds of winning inthe casino’s favor. This is what makesthe business profitable. There are a couple of measures that casinos and realcasino game developers use to reduce the player’sodds of winning. Below are some of the most common techniques used to make the game a little biased in favor of the house.

1. The casinos use high numbers decksto play blackjack. This increases the chances of streaks in the game. Althoughthere can be both winning and losing streaks, the odds of players getting winningstreaks are significantly less as shown in above sections.
2. Decks are shuffled at the end ofeach hand in versions of the game that are played with fewer numbers of decksof cards. Each time a hand is dealt from the deck the player’s odds of gettinga win increase. This is the same reason why in multi-deck blackjack games thecards are recut at 4.5 decks.
3. The most important factor that makesthe house edge in blackjack higher is that the player is the first to drawcards. This results in the player going bust even before the dealer can. Whenthe player busts the bet is lost in spite of the outcome of the dealer’s hand.So even if the dealer busts after the player the house has already won. Thisfeature increases the house edge from 8% to the current rates.

How to leverage BlackjackOdds to win More Real Money

Blackjackis one of the few gambling games where the use of strategy has succeeded in lowering the house edge. Some playersare now regular winners on blackjack tables online and at brick and mortarcasinos through the use of strategy.

Probability Of Winning Blackjack

Tips on howto beat the house at blackjack will improve your in-game decision-makinghelping you to win more. Below the reasons why blackjack favors the player andthousands of gamblers have made it their favorite game.

1. Thedealer is forced to hit at 16 meanwhile players can stand on 16. Therefore whenthe player sees the next cards can bust the hand they can force the dealer at16 to bust.
2. Inblackjack, the dealer is restricted in the actions that they cantake. The dealer cannot split hands ordouble down.
3. Wherethe player gets paid 3:2 or even better for a blackjack the house only gets 1:1for blackjack hands. This makes the game more rewarding to players.

Read these next:

• Gaming

  Gaming in Comfort and Style During COVID-19

• Gaming

  Do You Think Esports Are Stupid? Then This Article is for You